Koti » Psykologia » Vektori yhtä suuri kuin 1. Vektorit

Vektori yhtä suuri kuin 1. Vektorit

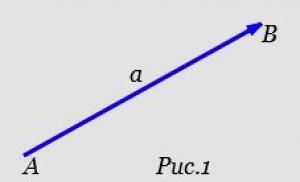
Vektori on euklidisessa avaruudessa olevan suoran suunnattu segmentti, jonka toista päätä (piste A) kutsutaan vektorin alusta ja toista päätä (piste B) vektorin lopuksi (kuva 1). Vektorit on merkitty:

Jos vektorin alku ja loppu ovat samat, vektoria kutsutaan nolla vektori ja on nimetty 0 .

Esimerkki. Olkoon vektorin alussa kaksiulotteisessa avaruudessa koordinaatit A(12.6) , ja vektorin loppu on koordinaatit B(12.6). Silloin vektori on nollavektori.

Osion pituus AB nimeltään moduuli (pituus, normi) -vektori ja sitä merkitään | a|. Kutsutaan vektoria, jonka pituus on yhtä suuri kuin yksi yksikkövektori. Moduulin lisäksi vektorille on tunnusomaista suunta: vektorilla on suunta alkaen A Vastaanottaja B. Vektoria kutsutaan vektoriksi, vastapäätä vektori.

Näitä kahta vektoria kutsutaan kollineaarinen, jos ne sijaitsevat samalla viivalla tai rinnakkaisilla viivoilla. Kuvassa fig. 3 punaista vektoria ovat kollineaarisia, koska ne sijaitsevat samalla suoralla, ja siniset vektorit ovat kollineaarisia, koska ne sijaitsevat yhdensuuntaisilla linjoilla. Kutsutaan kahta kollineaarista vektoria yhtä ohjattu, jos niiden päät ovat samalla puolella niiden alkua yhdistävää suoraa. Kutsutaan kahta kollineaarista vektoria vastakkaiseen suuntaan, jos niiden päät sijaitsevat niiden alkua yhdistävän suoran vastakkaisilla puolilla. Jos kaksi kollineaarista vektoria on samalla suoralla, niin niitä kutsutaan identtisesti suunnatuiksi, jos yksi yhden vektorin muodostamista säteistä sisältää kokonaan toisen vektorin muodostaman säteen. Muuten vektorien sanotaan olevan vastakkaisia. Kuvassa 3 siniset vektorit ovat samansuuntaisia ja punaiset vektorit vastakkaiseen suuntaan.

Näitä kahta vektoria kutsutaan yhtä suuri jos niillä on samat moduulit ja samat suunnat. Kuvassa 2 vektorit ovat yhtä suuret, koska niiden moduulit ovat samanarvoisia ja niillä on sama suunta.

Vektoreita kutsutaan koplanaarinen, jos ne sijaitsevat samassa tai yhdensuuntaisissa tasoissa.

SISÄÄN n Tarkastellaan dimensiovektoriavaruudessa kaikkien vektoreiden joukkoa, joiden aloituspiste on sama kuin koordinaattien origon. Sitten vektori voidaan kirjoittaa seuraavassa muodossa:

(1)

Missä x 1 , x 2 , ..., x n vektorin loppupisteen koordinaatit x.

Muotoon (1) kirjoitettua vektoria kutsutaan rivivektori, ja muotoon kirjoitettu vektori

(2)

nimeltään sarakevektori.

Määrä n nimeltään ulottuvuus (järjestyksessä) vektori. Jos silloin vektoria kutsutaan nolla vektori(vektorin aloituspisteestä lähtien ). Kaksi vektoria x Ja y ovat yhtä suuret silloin ja vain, jos niitä vastaavat elementit ovat yhtä suuret.

2018 Olshevsky Andrey Georgievich

Verkkosivusto täynnä kirjoja, voit ladata kirjoja

Vektorit tasossa ja avaruudessa, ongelmien ratkaisumenetelmiä, esimerkkejä, kaavoja

1 Vektorit avaruudessa

Avaruuden vektoreita ovat 10. luokan geometria, 11. luokan geometria ja analyyttinen geometria. Vektorien avulla voit ratkaista tehokkaasti Unified State Exam -testin toisen osan geometrisia ongelmia ja analyyttistä geometriaa avaruudessa. Vektorit avaruudessa annetaan samalla tavalla kuin vektorit tasossa, mutta kolmas koordinaatti z otetaan huomioon. Kolmannen ulottuvuuden avaruuden vektoreista poissulkeminen antaa vektoreita tasolla, jotka selitetään geometrialla 8., 9. luokalla.

1.1 Vektori tasossa ja avaruudessa

Vektori on suunnattu segmentti, jossa on alku ja loppu ja joka on kuvattu kuvassa nuolella. Satunnaista pistettä avaruudessa voidaan pitää nollavektorina. Nollavektorilla ei ole tiettyä suuntaa, koska alku ja loppu ovat samat, joten sille voidaan antaa mikä tahansa suunta.

Vektori englannista käännettynä tarkoittaa vektoria, suuntaa, kurssia, opastusta, suunnan asetusta, lentokonekurssia.

Nollasta poikkeavan vektorin pituus (moduuli) on janan AB pituus, joka on merkitty
. Vektorin pituus merkitty . Nollavektorin pituus on nolla = 0.

Nollasta poikkeavia vektoreita, jotka sijaitsevat samalla suoralla tai rinnakkaisilla viivoilla, kutsutaan kollineaarisiksi.

Nollavektori on kollineaarinen minkä tahansa vektorin kanssa.

Kollineaarisia nollasta poikkeavia vektoreita, joilla on sama suunta, kutsutaan yhteissuuntaisiksi. Samansuuntaiset vektorit on merkitty symbolilla . Esimerkiksi jos vektori on samansuuntainen vektorin kanssa , silloin käytetään merkintää.

Nollavektori on samansuuntainen minkä tahansa vektorin kanssa.

Vastakkaisesti suunnattuja on kaksi kollineaarista nollasta poikkeavaa vektoria, joilla on vastakkaiset suunnat. Vastakkaiset vektorit on merkitty merkillä ↓. Esimerkiksi jos vektori on suunnattu vastakkaisesti vektoriin nähden, käytetään merkintää ↓.

Samanpituisia yhteissuuntautuneita vektoreita kutsutaan yhtäläisiksi.

Monet fysikaaliset suureet ovat vektorisuureita: voima, nopeus, sähkökenttä.

Jos vektorin sovelluskohtaa (alkua) ei ole määritetty, se valitaan mielivaltaisesti.

Jos vektorin alku sijoitetaan pisteeseen O, niin vektorin katsotaan olevan viivästynyt pisteestä O. Mistä tahansa pisteestä voit piirtää yksittäisen vektorin, joka on yhtä suuri kuin tietty vektori.

1.2 Vektorisumma

Kun lisätään vektoreita kolmiosäännön mukaan, vedetään vektori 1, jonka päästä piirretään vektori 2, ja näiden kahden vektorin summa on vektori 3, joka on vedetty vektorin 1 alusta vektorin 2 loppuun:

Satunnaisille pisteille A, B ja C voit kirjoittaa vektorien summan:

+
=

Jos kaksi vektoria on peräisin samasta pisteestä

silloin on parempi lisätä ne suunnikkaan säännön mukaan.

Kun summataan kaksi vektoria suunnikkaan säännön mukaan, lisätyt vektorit asetetaan yhdestä pisteestä, näiden vektorien päistä suunnikkaat täydennetään soveltamalla toisen alkua yhden vektorin loppuun. Suunnikkaan diagonaalin muodostama vektori, joka on peräisin lisättävien vektorien alkupisteestä, on vektorien summa

Suunnikkasääntö sisältää erilaisen vektorien lisäysjärjestyksen kolmiosäännön mukaan.

Vektorien yhteenlaskennan lait:

1. Siirtymälaki + = +.

2. Yhdistelmälaki ( + ) + = + ( + ).

Jos on tarpeen lisätä useita vektoreita, niin vektorit lisätään pareittain tai monikulmiosäännön mukaisesti: vektori 2 piirretään vektorin 1 päästä, vektori 3 vedetään vektorin 2 päästä, vektori 4 vedetään vektorin 2 päästä. vektorin 3 loppu, vektori 5 vedetään vektorin 4 lopusta jne. Vektorin 1 alusta viimeisen vektorin loppuun vedetään vektori, joka on useiden vektorien summa.

Vektorien yhteenlaskennan lakien mukaan vektorien summausjärjestys ei vaikuta tuloksena olevaan vektoriin, joka on useiden vektorien summa.

Kahta nollasta poikkeavaa, samanpituista vastakkaisesti suunnattua vektoria kutsutaan vastakkaisiksi. Vector - on vektorin vastakohta

Nämä vektorit ovat vastakkaisia ja samansuuruisia.

1.3 Vektoriero

Vektoriero voidaan kirjoittaa vektorien summana

- = + (-),

missä "-" on vektorin vastainen vektori.

Vektorit ja - voidaan lisätä kolmio- tai suuntaviivasäännön mukaan.

Olkoon vektorit ja

Löytääksemme vektorien välisen eron, rakennamme vektorin -

Lisäämme vektorit ja - kolmiosäännön mukaan soveltaen vektorin alkua - vektorin loppuun, saamme vektorin + (-) = -

Lisäämme vektorit ja - suunnikkaan säännön mukaisesti - sivuun vektorien alun ja - yhdestä pisteestä

Jos vektorit ja ovat peräisin samasta pisteestä

silloin vektorien ero antaa niiden päät yhdistävän vektorin ja tuloksena olevan vektorin päässä oleva nuoli sijoitetaan sen vektorin suuntaan, josta toinen vektori vähennetään

Alla oleva kuva esittää yhteenlasku- ja vektorieroa

Alla oleva kuva havainnollistaa vektorien yhteenlaskua ja eroa eri tavoilla

Tehtävä. Vektorit ja ovat annettuja.

Piirrä vektorien summa ja erotus kaikilla mahdollisilla tavoilla kaikissa mahdollisissa vektoreiden yhdistelmissä.

1.4 Lemma kollineaarisilla vektoreilla

= k

1.5 Vektorin ja luvun tulo

Nollasta poikkeavan vektorin tulo luvulla k antaa vektorin = k, kollineaarisen vektorin kanssa. Vektorin pituus:

| | = |k |·| |

Jos k > 0, sitten vektorit ja ovat samansuuntaisia.

Jos k = 0, silloin vektori on nolla.

Jos k< 0, то векторы и противоположно направленные.

Jos | k | = 1, sitten vektorit ja ovat yhtä pitkiä.

Jos k = 1, silloin vektorit ovat yhtä suuret.

Jos k = -1, sitten vastakkaiset vektorit.

Jos | k | > 1, silloin vektorin pituus on suurempi kuin vektorin pituus.

Jos k > 1, silloin vektorit ovat molemmat samansuuntaisia ja pituus on suurempi kuin vektorin pituus.

Jos k< -1, то векторы и противоположно направленные и длина больше длины вектора .

Jos | k |< 1, то длина вектора меньше длины вектора .

Jos 0< k< 1, то векторы и сонаправленные и длина меньше длины вектора .

Jos -1< k< 0, то векторы и противоположно направленные и длина меньше длины вектора .

Nollavektorin ja luvun tulo antaa nollavektorin.

Tehtävä. Annettu vektori.

Rakenna vektorit 2, -3, 0,5, -1,5.

Tehtävä. Vektorit ja ovat annettuja.

Muodosta vektorit 3 + 2, 2 - 2, -2 -.

Lait, jotka kuvaavat vektorin kertomista luvulla

1. Yhdistelmälaki (kn) = k (n)

2. Ensimmäinen jakautumislaki k ( + ) = k + k .

3. Toinen jakautumislaki (k + n) = k + n.

Kollineaarisille vektoreille ja , jos ≠ 0, on yksi luku k, jonka avulla voit ilmaista vektorin seuraavasti:

= k

1.6 Samantasoiset vektorit

Samassa tai yhdensuuntaisissa tasoissa olevia vektoreita kutsutaan koplanaariseksi. Jos piirretään vektoreita, jotka ovat yhtä suuria kuin nämä samantasoiset vektorit yhdestä pisteestä, niin ne ovat samassa tasossa. Siksi voidaan sanoa, että vektoreita kutsutaan samantasoisiksi, jos samassa tasossa on yhtä suuria vektoreita.

Kaksi mielivaltaista vektoria ovat aina samassa tasossa. Nämä kolme vektoria voivat olla samassa tasossa tai ei-koplanaarisia. Kolme vektoria, joista vähintään kaksi on kollineaarisia, ovat samantasoisia. Kollineaariset vektorit ovat aina samassa tasossa.

1.7 Vektorin hajottaminen kahdeksi ei-kollineaariseksi vektoriksi

Mikä tahansa vektori hajoaa yksiselitteisesti tasossa kahdessa ei-kollineaarisessa nollasta poikkeavassa vektorissa Ja yhdellä laajennuskertoimella x ja y:

= x+y

Mikä tahansa vektori, joka on samassa tasossa nollasta poikkeavien vektorien kanssa ja voidaan yksiselitteisesti laajentaa kahdeksi ei-kollineaariseksi vektoriksi ja ainutlaatuisilla laajennuskertoimilla x ja y:

= x+y

Laajennetaan annettua vektoria tasossa annettujen ei-kollineaaristen vektoreiden mukaisesti ja:

Piirretään annetut koplanaariset vektorit yhdestä pisteestä

Vektorin lopusta piirretään vektorien kanssa yhdensuuntaisia viivoja, kunnes ne leikkaavat vektorien ja läpi piirrettyjen viivojen kanssa. Saamme suuntaviivan

Suunnikkaan sivujen pituudet saadaan kertomalla vektorien pituudet ja luvuilla x ja y, jotka määritetään jakamalla suunnikkaan sivujen pituudet niitä vastaavien vektoreiden pituuksilla ja. Saamme vektorin hajotuksen annettujen ei-kollineaaristen vektoreiden mukaan ja:

= x+y

Ratkaistavassa tehtävässä x ≈ 1.3, y ≈ 1.9, joten vektorin laajennus tietyissä ei-kollineaarisissa vektoreissa voidaan kirjoittaa muotoon

1,3 + 1,9 .

Ratkaistavassa tehtävässä x ≈ 1.3, y ≈ -1.9, joten vektorin laajennus tietyissä ei-kollineaarisissa vektoreissa voidaan kirjoittaa muotoon

1,3 - 1,9 .

1.8 Rinnakkaisputkisääntö

Suuntaissärmiö on kolmiulotteinen hahmo, jonka vastakkaiset pinnat koostuvat kahdesta samansuuntaisesta suunnikkaasta, jotka sijaitsevat yhdensuuntaisissa tasoissa.

Suuntasissärmiösäännön avulla voit lisätä kolme ei-tasossa olevaa vektoria, jotka piirretään yhdestä pisteestä, ja suuntaissärmiö rakennetaan siten, että summatut vektorit muodostavat sen reunat ja suuntaissärmiön loput reunat ovat vastaavasti samansuuntaisia ja yhtä pitkiä kuin summattujen vektoreiden muodostamat reunat. Suuntasärmiön lävistäjä muodostaa vektorin, joka on annettujen kolmen vektorin summa, joka alkaa summattavien vektorien origopisteestä.

1.9 Vektorin hajottaminen kolmeksi ei-tasoiseksi vektoriksi

Mikä tahansa vektori laajenee kolmeksi annetuksi ei-samantasoiseksi vektoriksi , ja yhdellä laajennuskertoimella x, y, z:

= x + y + z .

1.10 Suorakulmainen koordinaattijärjestelmä avaruudessa

Kolmiulotteisessa avaruudessa suorakaiteen muotoisen koordinaattijärjestelmän Oxyz määrittävät origo O ja leikkaavat keskenään kohtisuorat koordinaattiakselit Ox, Oy ja Oz valituilla positiivisilla suunnilla, jotka on merkitty nuolilla ja segmenttien mittayksiköllä. Jos segmenttien asteikko on sama kaikilla kolmella akselilla, niin tällaista järjestelmää kutsutaan karteesiseksi koordinaattijärjestelmäksi.

Koordinaatti x:tä kutsutaan abskissaksi, y on ordinaatti, z on aplikaatti. Pisteen M koordinaatit kirjoitetaan suluissa M (x; y; z).

1.11 Vektorikoordinaatit avaruudessa

Avaruudessa määritellään suorakaiteen muotoinen koordinaattijärjestelmä Oxyz. Koordinaattien origosta akselien Ox, Oy, Oz positiivisissa suunnissa piirretään vastaavat yksikkövektorit , , , joita kutsutaan koordinaattivektoreiksi ja jotka eivät ole samassa tasossa. Siksi mikä tahansa vektori hajotetaan kolmeksi annetuksi ei-samantasoiseksi koordinaattivektoriksi ja ainutlaatuisilla laajennuskertoimilla x, y, z:

= x + y + z .

Laajennuskertoimet x, y, z ovat vektorin koordinaatit tietyssä suorakaiteen muotoisessa koordinaatistossa, jotka on kirjoitettu sulkeisiin (x; y; z). Nollavektorin koordinaatit ovat yhtä suuret kuin nolla (0; 0; 0). Yhtäläisillä vektoreilla on samat vastaavat koordinaatit.

Säännöt tuloksena olevan vektorin koordinaattien löytämiseksi:

1. Kun summataan kaksi tai useampia vektoreita, tuloksena olevan vektorin kukin koordinaatti on yhtä suuri kuin annettujen vektorien vastaavien koordinaattien summa. Jos annetaan kaksi vektoria (x 1 ; y 1 ; z 1) ja (x 1 ; y 1 ; z 1), niin vektorien + summa antaa vektorin, jonka koordinaatit (x 1 + x 1; y 1 + y) 1 ; z 1 + z 1)

+ = (x 1 + x 1; y1 + y1; z 1 + z 1)

2. Ero on eräänlainen summa, joten vastaavien koordinaattien erotus antaa kunkin vektorin koordinaatin, joka saadaan vähentämällä kaksi annettua vektoria. Jos annetaan kaksi vektoria (x a; y a; z a) ja (x b; y b; z b), niin vektorien erotus antaa vektorin, jolla on koordinaatit (x a - x b; y a - y b; z a - z b)

- = (x a - x b; y a - y b; z a - z b)

3. Kun vektori kerrotaan luvulla, jokainen tuloksena olevan vektorin koordinaatti on yhtä suuri kuin tämän luvun ja annetun vektorin vastaavan koordinaatin tulo. Jos luku k ja vektori (x; y; z) on annettu, niin kertomalla vektori luvulla k saadaan vektori k koordinaatteineen

k = (kx; ky; kz).

Tehtävä. Selvitä vektorin koordinaatit = 2 - 3 + 4, jos vektorien koordinaatit ovat (1; -2; -1), (-2; 3; -4), (-1; -3; 2).

Ratkaisu

2 + (-3) + 4

2 = (2·1; 2·(-2); 2·(-1)) = (2; -4; -2);

3 = (-3 (-2); -3,3; -3 (-4)) = (6; -9; 12);

4 = (4·(-1); 4·(-3); 4,2) = (-4; -12; 8).

= (2 + 6 - 4; -4 - 9 -12; -2 + 12 + 8) = (4; -25; 18).

1.12 Vektorin, sädevektorin ja pisteen koordinaatit

Vektorin koordinaatit ovat vektorin lopun koordinaatit, jos vektorin alku sijoitetaan origoon.

Sädevektori on origosta tiettyyn pisteeseen piirretty vektori, jonka sädevektorin ja pisteen koordinaatit ovat yhtä suuret.

Jos vektori
on annettu pisteillä M 1 (x 1 ; y 1 ; z 1) ja M 2 (x 2 ; y 2 ; z 2), silloin kukin sen koordinaateista on yhtä suuri kuin lopun ja vastaavien koordinaattien erotus. vektorin alku

Kollineaarisille vektoreille = (x 1 ; y 1 ; z 1) ja = (x 2 ; y 2 ; z 2), jos ≠ 0, on yksi luku k, jonka avulla voit ilmaista vektorin seuraavasti:

= k

Sitten vektorin koordinaatit ilmaistaan vektorin koordinaattien kautta

= (kx 1; ky 1; kz 1)

Kollineaaristen vektoreiden vastaavien koordinaattien suhde on yhtä suuri kuin singulaariluku k

1.13 Vektorin pituus ja kahden pisteen välinen etäisyys

Vektorin pituus (x; y; z) on yhtä suuri kuin sen koordinaattien neliösumman neliöjuuri

Alkupisteiden M 1 (x 1 ; y 1 ; z 1) ja loppupisteiden M 2 (x 2 ; y 2 ; z 2) määrittämän vektorin pituus on yhtä suuri kuin summan neliöjuuri. vektorin lopun ja alun vastaavien koordinaattien välisen eron neliöt

Etäisyys d kahden pisteen M 1 (x 1 ; y 1 ; z 1) ja M 2 (x 2 ; y 2 ; z 2) välillä on yhtä suuri kuin vektorin pituus

Tasossa ei ole z-koordinaattia

Pisteiden M 1 (x 1 ; y 1) ja M 2 (x 2 ; y 2) välinen etäisyys

1.14 Jakson keskikohdan koordinaatit

Jos kohta C on janan AB keskikohta, jolloin pisteen C sädevektori mielivaltaisessa koordinaatistossa, jonka origo on pisteessä O, on yhtä suuri kuin puolet pisteiden A ja B sädevektorien summasta

Jos vektorien koordinaatit
(x; y; z),
(x 1 ; y 1 ; z 1),
(x 2 ; y 2 ; z 2), silloin jokainen vektorin koordinaatti on yhtä suuri kuin puolet vastaavien vektorin koordinaattien summasta ja

,
,

= (x, y, z) =

Jokainen janan keskikohdan koordinaateista on yhtä suuri kuin puolet janan päiden vastaavien koordinaattien summasta.

1.15 Vektorien välinen kulma

Vektorien välinen kulma on yhtä suuri kuin yhdestä pisteestä vedettyjen ja näiden vektoreiden kanssa suunnattujen säteiden välinen kulma. Vektorien välinen kulma voi olla 0 0 - 180 0, mukaan lukien. Samansuuntaisten vektoreiden välinen kulma on 0 0 . Jos yksi vektori tai molemmat ovat nollia, niin vektorien välinen kulma, joista ainakin yksi on nolla, on 0 0 . Pystysuorien vektorien välinen kulma on 90 0. Vastakkaisten vektorien välinen kulma on 180 0.

1.16 Vektoriprojektio

1.17 Vektorien pistetulo

Kahden vektorin skalaaritulo on luku (skalaari), joka on yhtä suuri kuin vektorien pituuksien ja vektorien välisen kulman kosinin tulo

Jos = 0 0, silloin vektorit ovat samansuuntaisia
Ja
= cos 0 0 = 1, joten samansuuntaisten vektorien skalaaritulo on yhtä suuri kuin niiden pituuksien (moduulien) tulo

Jos vektorien välinen kulma on 0< < 90 0 , то косинус угла между такими векторами больше нуля
, siksi skalaaritulo on suurempi kuin nolla
.

Jos nollasta poikkeavat vektorit ovat kohtisuorassa, niin niiden skalaaritulo on yhtä suuri kuin nolla
, koska cos 90 0 = 0. Kohtisuorien vektorien skalaaritulo on yhtä suuri kuin nolla.

Jos
, silloin tällaisten vektorien välisen kulman kosini on pienempi kuin nolla
, siksi skalaaritulo on pienempi kuin nolla
.

Vektorien välisen kulman kasvaessa niiden välisen kulman kosini
pienenee ja saavuttaa minimiarvon = 180 0, kun vektorit ovat vastakkaisia
. Koska cos 180 0 = -1, niin
. Vastakkaisten vektorien skalaaritulo on yhtä suuri kuin niiden pituuksien (moduulien) negatiivinen tulo.

Vektorin skalaarineliö on yhtä suuri kuin vektorin neliömoduuli

Niiden vektorien pistetulo, joista ainakin yksi on nolla, on yhtä suuri kuin nolla.

1.18 Vektorien skalaaritulon fyysinen merkitys

Fysiikan kurssista tiedetään, että A voiman tekemä työ kehoa liikutettaessa yhtä suuri kuin voima- ja siirtymävektorien pituuksien ja niiden välisen kulman kosinin tulo, eli yhtä suuri kuin voima- ja siirtymävektorien skalaaritulo

Jos voimavektori on samansuuntainen kappaleen liikkeen kanssa, niin vektorien välinen kulma
= 0 0, joten siirtymävoiman tekemä työ on maksimi ja yhtä suuri kuin A =
.

Jos 0< < 90 0 , то работа силы на перемещении положительна A > 0.

Jos = 90 0, niin siirtymävoiman tekemä työ on nolla A = 0.

Jos 90 0< < 180 0 , то работа силы на перемещении отрицательна A < 0.

Jos voimavektori on suunnattu vastakkain kappaleen liikettä vastaan, niin vektorien välinen kulma = 180 0, joten voiman työ liikkeeseen on negatiivinen ja yhtä suuri kuin A = -.

Tehtävä. Määritä painovoiman tekemä työ nostettaessa 1 tonnin painoista henkilöautoa 1 km pitkää tietä pitkin, jonka kaltevuuskulma on 30 0 horisonttiin nähden. Kuinka monta litraa vettä lämpötilassa 20 0 voidaan keittää tällä energialla?

Ratkaisu

Job Painovoima kappaletta liikutettaessa se on yhtä suuri kuin vektorien pituuksien ja niiden välisen kulman kosinin tulo, eli yhtä suuri kuin painovoima- ja siirtymävektorien skalaaritulo

Painovoima

G = mg = 1000 kg 10 m/s 2 = 10 000 N.

= 1000 m.

Kulma vektorien välillä = 120 0 . Sitten

cos 120 0 = cos (90 0 + 30 0) = - sin 30 0 = - 0,5.

Korvataan

A = 10 000 N · 1 000 m · (-0,5) = - 5 000 000 J = - 5 MJ.

1.19 Koordinaattien vektorien pistetulo

Kahden vektorin pistetulo = (x1; y1; z1) ja = (x 2 ; y 2 ; z 2) suorakaiteen muotoisessa koordinaattijärjestelmässä on yhtä suuri kuin samannimisen koordinaattien tulojen summa

= x 1 x 2 + y 1 y 2 + z 1 z 2 .

1.20 Vektorien kohtisuoran ehto

Jos nollasta poikkeavat vektorit = (x 1 ; y 1 ; z 1) ja = (x 2 ; y 2 ; z 2) ovat kohtisuorassa, niin niiden skalaaritulo on nolla

Jos annetaan yksi nollasta poikkeava vektori = (x 1 ; y 1 ; z 1), niin siihen nähden kohtisuorassa (normaalissa) olevan vektorin koordinaattien = (x 2 ; y 2 ; z 2) on täytettävä yhtäläisyys

x 1 x 2 + y 1 y 2 + z 1 z 2 = 0.

Tällaisia vektoreita on ääretön määrä.

Jos tasossa on yksi nollasta poikkeava vektori = (x 1 ; y 1), niin siihen nähden kohtisuorassa (normaalissa) = (x 2 ; y 2) olevan vektorin koordinaattien on täytettävä yhtäläisyys

x 1 x 2 + y 1 y 2 = 0.

Jos tasossa on nollasta poikkeava vektori = (x 1 ; y 1), niin riittää, että asetetaan mielivaltaisesti jokin vektorin koordinaateista kohtisuoraan (normaali) = (x 2 ; y 2) ja siitä vektorien kohtisuoran ehto

x 1 x 2 + y 1 y 2 = 0

ilmaisee vektorin toisen koordinaatin.

Jos esimerkiksi korvaat mielivaltaisen koordinaatin x 2, niin

y 1 y 2 = - x 1 x 2 .

Toinen vektorin koordinaatti

Jos annamme x 2 = y 1, niin vektorin toinen koordinaatti

Jos tasossa on nollasta poikkeava vektori = (x 1 ; y 1), niin siihen nähden kohtisuorassa (normaalissa) oleva vektori = (y 1 ; -x 1).

Jos yksi nollasta poikkeavan vektorin koordinaateista on nolla, niin vektorilla on sama koordinaatti, joka ei ole nolla, ja toinen koordinaatti on yhtä suuri kuin nolla. Tällaiset vektorit sijaitsevat koordinaattiakseleilla ja ovat siksi kohtisuorassa.

Määritellään toinen vektori, joka on kohtisuorassa vektoriin = (x 1 ; y 1), mutta vastapäätä vektoria , eli vektori - . Sitten riittää, että muutetaan vektorin koordinaattien etumerkkejä

- = (-y1; x 1)

1 = (y1; -x 1),

2 = (-y1; x 1).

Tehtävä.

Ratkaisu

Kahden vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin = (x 1 ; y 1) tasossa

1 = (y1; -x 1),

2 = (-y1; x 1).

Korvaava vektorin koordinaatit = (3; -5)

1 = (-5; -3),

2 = (-(-5); 3) = (5; 3).

x 1 x 2 + y 1 y 2 = 0

3·(-5) + (-5)·(-3) = -15 + 15 = 0

oikein!

3 · 5 + (-5) · 3 = 15 - 15 = 0

oikein!

Vastaus: 1 = (-5; -3), 2 = (5; 3).

Jos annamme x 2 = 1, korvaa

x 1 + y 1 y 2 = 0.

y 1 y 2 = -x 1

Saadaan vektorin koordinaatti y 2, joka on kohtisuorassa vektoriin = (x 1 ; y 1)

Saadaksesi toinen vektori, joka on kohtisuorassa vektoriin nähden = (x 1 ; y 1), mutta vastapäätä vektoria . Antaa

Sitten riittää, että muutetaan vektorin koordinaattien etumerkkejä.

Kahden vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin = (x 1 ; y 1) tasossa

Tehtävä. Annettu vektori = (3; -5). Etsi kaksi eri suuntaista normaalivektoria.

Ratkaisu

Kahden vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin = (x 1 ; y 1) tasossa

Yhden vektorin koordinaatit

Toisen vektorin koordinaatit

Vektorien kohtisuoran tarkistamiseksi korvaamme niiden koordinaatit vektorien kohtisuoran ehtoon

x 1 x 2 + y 1 y 2 = 0

3 1 + (-5) 0,6 = 3 - 3 = 0

oikein!

3·(-1) + (-5)·(-0,6) = -3 + 3 = 0

oikein!

Vastaus: ja.

Jos määrität x 2 = - x 1 , korvaa se

x 1 (-x 1) + y 1 y 2 = 0.

-x 1 2 + y 1 y 2 = 0.

y 1 y 2 = x 1 2

Saamme vektorin koordinaatin kohtisuorassa vektoriin nähden

Jos määrität x 2 = x 1 , korvaa se

x 1 x 1 + y 1 y 2 = 0.

x 1 2 + y 1 y 2 = 0.

y 1 y 2 = -x 1 2

Saadaan toisen vektorin y-koordinaatti, joka on kohtisuorassa vektoriin nähden

Yhden vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin nähden tasossa = (x 1 ; y 1)

Toisen vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin nähden tasossa = (x 1 ; y 1)

Kahden vektorin koordinaatit, jotka ovat kohtisuorassa vektoriin = (x 1 ; y 1) tasossa

1.21 Vektorien välisen kulman kosini

Kahden nollasta poikkeavan vektorin välisen kulman kosini = (x 1 ; y 1 ; z 1) ja = (x 2 ; y 2 ; z 2) on yhtä suuri kuin vektorien skalaaritulo jaettuna vektorin tulolla näiden vektorien pituudet

Jos
= 1, silloin vektorien välinen kulma on 0 0, vektorit ovat samansuuntaisia.

Jos 0< < 1, то 0 0 < < 90 0 .

Jos = 0, niin vektorien välinen kulma on 90 0, vektorit ovat kohtisuorassa.

Jos -1< < 0, то 90 0 < < 180 0 .

Jos = -1, niin vektorien välinen kulma on 180 0, vektorit ovat vastakkaisia.

Jos vektori annetaan alun ja lopun koordinaateilla, niin alun koordinaatit vähentämällä vektorin lopun vastaavista koordinaateista saadaan tämän vektorin koordinaatit.

Tehtävä. Etsi vektorien välinen kulma (0; -2; 0), (-2; 0; -4).

Ratkaisu

Vektorien pistetulo

= 0·(-2) + (-2)·0 + 0·(-4) = 0,

siksi vektorien välinen kulma on yhtä suuri kuin = 90 0 .

1.22 Vektorien skalaaritulon ominaisuudet

Skalaarituotteen ominaisuudet ovat voimassa mille tahansa , , , k :

1.
, Jos
, Tuo
, Jos =, Tuo
= 0.

2. Matkalaki

3. Jakelulaki

4. Yhdistelmälaki
.

1.23 Suora vektori

Suoran suuntavektori on nollasta poikkeava vektori, joka sijaitsee suoralla tai tietyn suoran suuntaisella suoralla.

Jos suora määritetään kahdella pisteellä M 1 (x 1 ; y 1 ; z 1) ja M 2 (x 2 ; y 2 ; z 2), niin ohjain on vektori
tai sen vastakkainen vektori
= - , jonka koordinaatit

On suositeltavaa asettaa koordinaattijärjestelmä siten, että suora kulkee koordinaattien origon kautta, jolloin suoran ainoan pisteen koordinaatit ovat suuntavektorin koordinaatit.

Tehtävä. Määritä pisteiden M 1 (1; 0; 0), M 2 (0; 1; 0) kautta kulkevan suoran suuntavektorin koordinaatit.

Ratkaisu

Pisteiden M 1 (1; 0; 0), M 2 (0; 1; 0) kautta kulkevan suoran suuntavektoria on merkitty
. Jokainen sen koordinaateista on yhtä suuri kuin vektorin lopun ja alun vastaavien koordinaattien välinen ero

= (0 - 1; 1 - 0; 0 - 0) = (-1; 1; 0)

Kuvataan sellaisen suoran suuntavektori koordinaattijärjestelmässä, jonka alku on pisteessä M 1, loppu pisteessä M 2 ja yhtä suuri vektori
lähtöpisteestä, jonka pää on pisteessä M (-1; 1; 0)

1.24 Kahden suoran välinen kulma

Mahdolliset vaihtoehdot kahden suoran suhteelliselle sijainnille tasossa ja tällaisten suorien väliselle kulmille:

1. Suorat leikkaavat yhdessä pisteessä muodostaen 4 kulmaa, 2 paria pystykulmia on yhtä suuria pareittain. Kahden leikkaavan suoran välinen kulma φ on kulma, joka ei ylitä kolmea muuta näiden viivojen välistä kulmaa. Siksi viivojen välinen kulma on φ ≤ 90 0.

Leikkaavat suorat voivat olla erityisesti kohtisuorassa φ = 90 0:aan nähden.

Mahdolliset vaihtoehdot kahden suoran suhteelliselle sijainnille avaruudessa ja tällaisten suorien väliselle kulmille:

2. Suorat ovat yhdensuuntaisia, eli ne eivät kohtaa eivätkä leikkaa, φ=0 0 .

3. Suorat osuvat yhteen, φ = 0 0 .

4. Suorat leikkaavat, eli ne eivät leikkaa avaruudessa eivätkä ole yhdensuuntaisia. Leikkaavien viivojen välinen kulma φ on kulma näiden viivojen rinnalle piirrettyjen viivojen välillä siten, että ne leikkaavat. Siksi viivojen välinen kulma on φ ≤ 90 0.

Kahden suoran välinen kulma on sama kuin näiden samassa tasossa olevien suorien rinnalle piirrettyjen suorien välinen kulma. Siksi viivojen välinen kulma on 0 0 ≤ φ ≤ 90 0.

Kulma θ (theta) vektorien ja 0 0 ≤ θ ≤ 180 0 välillä.

Jos viivojen α ja β välinen kulma φ on yhtä suuri kuin näiden viivojen suuntavektorien välinen kulma θ φ = θ, niin

cos φ = cos θ.

Jos suorien välinen kulma on φ = 180 0 - θ, niin

cos φ = cos (180 0 - θ) = - cos θ.

cos φ = - cos θ.

Siksi suorien viivojen välisen kulman kosini on yhtä suuri kuin vektorien välisen kulman kosinin moduuli

cos φ = |cos θ|.

Jos nollasta poikkeavien vektorien koordinaatit = (x 1 ; y 1 ; z 1) ja = (x 2 ; y 2 ; z 2) on annettu, niin niiden välisen kulman θ kosini

Viivojen välisen kulman kosini on yhtä suuri kuin näiden viivojen suuntavektorien välisen kulman kosinin moduuli

cos φ = |cos θ| =

Viivat ovat samoja geometrisia objekteja, joten samat trigonometriset cos-funktiot ovat läsnä kaavassa.

Jos kukin kahdesta suorasta on annettu kahdella pisteellä, on mahdollista määrittää näiden viivojen suuntavektorit ja viivojen välisen kulman kosini.

Jos cos φ = 1, silloin viivojen välinen kulma φ on 0 0, näille suorille voidaan ottaa yksi näiden viivojen suuntavektorista, suorat ovat yhdensuuntaiset tai yhtenevät. Jos suorat eivät ole samat, ne ovat yhdensuuntaisia. Jos suorat ovat samat, mikä tahansa piste yhdellä viivalla kuuluu toiselle suoralle.

Jos 0< cos φ ≤ 1, niin viivojen välinen kulma on 0 0< φ ≤ 90 0 , прямые пересекаются или скрещиваются. Если прямые не пересекаются, то они скрещиваются. Если прямые пересекаются, то они имеют общую точку.

Jos cos φ = 0, silloin suorien välinen kulma φ on 90 0 (suorat ovat kohtisuorassa), suorat leikkaavat tai leikkaavat.

Tehtävä. Määritä suorien M 1 M 3 ja M 2 M 3 välinen kulma pisteiden M 1 (1; 0; 0), M 2 (0; 1; 0) ja M 3 (0; 0; 1) koordinaateilla.

Ratkaisu

Muodostetaan annetut pisteet ja suorat Oxyz-koordinaattijärjestelmään.

Suuntaamme viivojen suuntavektorit siten, että vektoreiden välinen kulma θ osuu yhteen annettujen viivojen välisen kulman φ kanssa. Esitetään vektoreita =
ja =
, sekä kulmat θ ja φ:

Määritetään vektorien ja koordinaatit

= = (1 - 0; 0 - 0; 0 - 1) = (1; 0; -1);

= = (0 - 0; 1 - 0; 0 - 1) = (0; 1; -1). d = 0 ja ax + by + cz = 0;

Taso on yhdensuuntainen koordinaattiakselin kanssa, jonka merkintä puuttuu tason yhtälöstä ja siksi vastaava kerroin on nolla, esimerkiksi kun c = 0, taso on yhdensuuntainen Oz-akselin kanssa eikä sisältävät z yhtälössä ax + by + d = 0;

Taso sisältää sen koordinaattiakselin, jonka merkintä puuttuu, joten vastaava kerroin on nolla ja d = 0, esimerkiksi kun c = d = 0, taso on yhdensuuntainen Oz-akselin kanssa eikä sisällä z:tä yhtälö ax + by = 0;

Taso on yhdensuuntainen koordinaattitason kanssa, jonka symbolit puuttuvat tason yhtälöstä ja siksi vastaavat kertoimet ovat nolla, esimerkiksi kun b = c = 0, taso on yhdensuuntainen koordinaattitason Oyz kanssa eikä sisällä y, z yhtälössä ax + d = 0.

Jos taso osuu yhteen koordinaattitason kanssa, niin tällaisen tason yhtälö on annettuun koordinaattitasoon nähden kohtisuorassa olevan koordinaattiakselin merkinnän nolla, esimerkiksi kun x = 0, annettu taso on koordinaattitaso Oyz.

Tehtävä. Normaalivektori saadaan yhtälöstä

Esitä tason yhtälö normaalimuodossa.

Ratkaisu

Normaalivektorikoordinaatit

A; b; c), sitten voit korvata tason yleisen yhtälön pisteen M 0 (x 0 ; y 0 ; z 0) koordinaatit ja normaalivektorin koordinaatit a, b, c

ax + by + cz + d = 0 (1)

Saadaan yhtälö, jossa on yksi tuntematon d

ax 0 + x 0 + cz 0 + d = 0

Täältä

d = -(ax 0 + x 0 + cz 0 )

Tasoyhtälö (1) d:n korvaamisen jälkeen

ax + by + cz - (ax 0 + by 0 + cz 0) = 0

Saamme pisteen M 0 (x 0 ; y 0 ; z 0) läpi kulkevan tason yhtälön, joka on kohtisuorassa nollasta poikkeavaan vektoriin nähden (a; b; c)

a (x - x 0) + b (y - y 0) + c (z - z 0) = 0

Avataan sulut

ax - ax 0 + by - by 0 + cz - cz 0 = 0

ax + by + cz - ax 0 - by 0 - cz 0 = 0

Merkitään

d = - ax 0 - 0 - cz 0

Saamme tason yleisen yhtälön

ax + by + cz + d = 0.

1.29 Kahden pisteen ja origon kautta kulkevan tason yhtälö

ax + by + cz + d = 0.

On suositeltavaa asettaa koordinaattijärjestelmä siten, että taso kulkee tämän koordinaattijärjestelmän origon kautta. Tässä tasossa olevat pisteet M 1 (x 1 ; y 1 ; z 1) ja M 2 (x 2 ; y 2 ; z 2) on määritettävä siten, että näitä pisteitä yhdistävä suora viiva ei kulje origon kautta.

Taso kulkee origon läpi, joten d = 0. Tällöin tason yleinen yhtälö saa muodon

ax + by + cz = 0.

Tuntemattomia kertoimia a, b, c on 3 kappaletta. Korvaamalla kahden pisteen koordinaatit tason yleisyhtälöön saadaan 2 yhtälöjärjestelmä. Jos otamme jonkin kertoimen tason yleisestä yhtälöstä yhtä suureksi kuin yksi, niin 2 yhtälöjärjestelmä antaa meille mahdollisuuden määrittää 2 tuntematonta kerrointa.

Jos yksi pisteen koordinaateista on nolla, niin tätä koordinaattia vastaava kerroin otetaan yhdeksi.

Jos jollakin pisteellä on kaksi nollakoordinaatista, niin yhtä näistä nollakoordinaateista vastaava kerroin otetaan yhdeksi.

Jos a = 1 hyväksytään, niin kahden yhtälön järjestelmä antaa meille mahdollisuuden määrittää 2 tuntematonta kerrointa b ja c:

Näiden yhtälöiden järjestelmä on helpompi ratkaista kertomalla jokin yhtälö sellaisella luvulla, että joidenkin tuntemattomien kertoimet ovat yhtä suuret. Sitten yhtälöiden ero antaa meille mahdollisuuden eliminoida tämä tuntematon ja määrittää toinen tuntematon. Korvaamalla löydetyn tuntemattoman mihin tahansa yhtälöön voit määrittää toisen tuntemattoman.

1.30 Kolmen pisteen läpi kulkevan tason yhtälö

Määritetään tason yleisen yhtälön kertoimet

ax + by + cz + d = 0,

kulkee pisteiden M 1 (x 1 ; y 1 ; z 1 ), M 2 (x 2 ; y 2 ; z 2) ja M 3 (x 3 ; y 3 ; z 3) läpi. Pisteillä ei saa olla kahta identtistä koordinaattia.

Tuntemattomia kertoimia a, b, c ja d on neljä. Korvaamalla kolmen pisteen koordinaatit tason yleisyhtälöön saadaan 3 yhtälöjärjestelmä. Ota jokin kerroin tason yleisestä yhtälöstä, joka on yhtä suuri kuin yksikkö, niin 3 yhtälöjärjestelmän avulla voit määrittää 3 tuntematonta kerrointa. Yleensä a = 1 hyväksytään, silloin 3 yhtälöjärjestelmä antaa meille mahdollisuuden määrittää 3 tuntematonta kerrointa b, c ja d:

On parempi ratkaista yhtälöjärjestelmä eliminoimalla tuntemattomat (Gaussin menetelmä). Voit järjestää yhtälöt uudelleen järjestelmässä. Mikä tahansa yhtälö voidaan kertoa tai jakaa millä tahansa kertoimella, joka ei ole nolla. Mikä tahansa kaksi yhtälöä voidaan lisätä ja tuloksena oleva yhtälö voidaan kirjoittaa jommankumman lisätyn yhtälön tilalle. Tuntemattomat suljetaan pois yhtälöistä hankkimalla niiden eteen nollakerroin. Yhdessä yhtälössä, yleensä alimmassa, on jäljellä yksi muuttuja, joka määritetään. Löytynyt muuttuja korvataan toisella yhtälöllä alhaalta, jolloin jää yleensä 2 tuntematonta. Yhtälöt ratkaistaan alhaalta ylös ja kaikki tuntemattomat kertoimet määritetään.

Kertoimet asetetaan tuntemattomien eteen ja tuntemattomista vapaat termit siirretään yhtälöiden oikealle puolelle

Ylärivi sisältää yleensä yhtälön, jonka kerroin on 1 ennen ensimmäistä tai mitä tahansa tuntematonta, tai koko ensimmäinen yhtälö on jaettu kertoimella ennen ensimmäistä tuntematonta. Tässä yhtälöjärjestelmässä jaa ensimmäinen yhtälö y 1:llä

Ennen ensimmäistä tuntematonta saimme kertoimen 1:

Nollataksesi kertoimen toisen yhtälön ensimmäisen muuttujan edessä, kerro ensimmäinen yhtälö -y 2:lla, lisää se toiseen yhtälöön ja kirjoita tuloksena oleva yhtälö toisen yhtälön sijaan. Ensimmäinen tuntematon toisesta yhtälöstä eliminoidaan, koska

y 2 b - y 2 b = 0.

Samoin eliminoimme kolmannen yhtälön ensimmäisen tuntemattoman kertomalla ensimmäisen yhtälön -y 3:lla, lisäämällä sen kolmanteen yhtälöön ja kirjoittamalla tuloksena olevan yhtälön kolmannen yhtälön sijaan. Kolmannen yhtälön ensimmäinen tuntematon eliminoidaan myös, koska

y 3 b - y 3 b = 0.

Samoin eliminoimme toisen tuntemattoman kolmannesta yhtälöstä. Ratkaisemme järjestelmän alhaalta ylöspäin.

Tehtävä.

ax + by + cz + d = 0,

kulkee pisteiden M 1 (0; 0; 0), M 2 (0; 1; 0) ja y kautta+ 0 z + 0 = 0

x = 0.

Määritetty taso on koordinaattitaso Oyz.

Tehtävä. Määritä tason yleinen yhtälö

ax + by + cz + d = 0,

kulkee pisteiden M1 (1; 0; 0), M2 (0; 1; 0) ja M3 (0; 0; 1) läpi. Etsi etäisyys tästä tasosta pisteeseen M 0 (10; -3; -7).

Ratkaisu

Muodostetaan annetut pisteet Oxyz-koordinaattijärjestelmään.

Hyväksytään a= 1. Korvaamalla kolmen pisteen koordinaatit tason yleisyhtälöön saadaan 3 yhtälöjärjestelmä

ℓ =

Verkkosivut: 1 2 Vektorit tasossa ja avaruudessa (jatkuu)

Neuvottelut Andrey Georgievich Olshevskyn kanssa Skype da.kiusata.ru

Matematiikan, fysiikan, tietojenkäsittelytieteen opiskelijoiden ja koululaisten, paljon pisteitä (osa C) saavien koululaisten ja heikkojen opiskelijoiden valmistaminen valtionkokeeseen (GIA) ja yhtenäiseen valtionkokeeseen. Samanaikainen nykyisen akateemisen suorituskyvyn parantaminen kehittämällä muistia, ajattelua ja selkeää selitystä esineiden monimutkaisista visuaalisista esityksistä. Jokaista opiskelijaa kohtaan erityinen lähestymistapa. Valmistautuminen olympialaisiin, jotka tarjoavat pääsyn etuja. 15 vuoden kokemus oppilaiden suoritusten parantamisesta.

Korkeampi matematiikka, algebra, geometria, todennäköisyysteoria, matemaattinen tilasto, lineaarinen ohjelmointi.

Selkeä teorian selitys, ymmärrysaukkojen kurominen, opetusmenetelmät ongelmien ratkaisemiseksi, konsultointi kurssitöiden ja tutkintojen kirjoittamisessa.

Lento-, raketti- ja automoottorit. Hypersonic, ramjet, raketti, pulssiräjäytys, sykkivä, kaasuturbiini, mäntäpolttomoottorit - teoria, suunnittelu, laskelma, lujuus, suunnittelu, valmistustekniikka. Termodynamiikka, lämpötekniikka, kaasudynamiikka, hydrauliikka.

Ilmailu, aeromekaniikka, aerodynamiikka, lentodynamiikka, teoria, suunnittelu, aerohydromekaniikka. Ultrakevyet lentokoneet, ekranoplanit, lentokoneet, helikopterit, raketit, risteilyohjukset, ilmatyynyalukset, ilmalaivat, potkurit - teoria, suunnittelu, laskelma, lujuus, suunnittelu, valmistustekniikka.

Ideoiden luominen ja toteutus. Tieteellisen tutkimuksen perusteet, generointimenetelmät, tieteellisten, kekseliäisten, liikeideoiden toteuttaminen. Opetustekniikoita tieteellisten ongelmien ja keksinnöllisten ongelmien ratkaisemiseen. Tieteellinen, kekseliäs, kirjoittaminen, insinööriluovuus. Lausunto, valinta, arvokkaimpien tieteellisten, kekseliäisten ongelmien ja ideoiden ratkaisu.

Luovien tulosten julkaiseminen. Kuinka kirjoittaa ja julkaista tieteellinen artikkeli, hakea keksintöä, kirjoittaa, julkaista kirja. Kirjoittamisen teoria, väitöskirjat. Rahan ansaitseminen ideoilla ja keksinnöillä. Keksintöjen luomiseen liittyvä konsultointi, keksintöhakemusten kirjoittaminen, tieteelliset artikkelit, keksintöhakemukset, kirjat, monografiat, väitöskirjat. Keksintöjen, tieteellisten artikkelien, monografioiden yhteistekijä.

Teoreettinen mekaniikka (teormekh), materiaalien lujuus (materiaalien lujuus), koneen osat, mekanismien ja koneiden teoria (TMM), koneenrakennustekniikka, tekniset tieteet.

Sähkötekniikan (TOE) teoreettiset perusteet, elektroniikka, digitaalisen ja analogisen elektroniikan perusteet.

Analyyttinen geometria, kuvaava geometria, suunnittelugrafiikka, piirustus. Tietokonegrafiikka, grafiikkaohjelmointi, piirustukset AutoCADissa, NanoCAD, valokuvamontaasi.

Logiikka, kaaviot, puut, diskreetti matematiikka.

OpenOffice ja LibreOffice Basic, Visual Basic, VBA, NET, ASP.NET, makrot, VBScript, BASIC, C, C++, Delphi, Pascal, Delphi, Pascal, C#, JavaScript, Fortran, html, Matkad. Ohjelmien, pelien luominen tietokoneille, kannettaville tietokoneille, mobiililaitteille. Ilmaisten valmiiden ohjelmien, avoimen lähdekoodin moottoreiden käyttö.

Verkkosivustojen luominen, sijoittaminen, edistäminen, ohjelmointi, verkkokaupat, rahan ansaitseminen verkkosivuilla, web-suunnittelu.

Tietojenkäsittelytiede, PC-käyttäjä: tekstit, taulukot, esitykset, nopeuskirjoituksen koulutus 2 tunnissa, tietokannat, 1C, Windows, Word, Excel, Access, Gimp, OpenOffice, AutoCAD, nanoCad, Internet, verkot, sähköposti.

Kiinteiden tietokoneiden ja kannettavien tietokoneiden asennus ja korjaus.

Videobloggaaja, luo, muokkaa, julkaisee videoita, muokkaa videoita, ansaitsee rahaa videoblogeista.

Valinta, tavoitteiden saavuttaminen, suunnittelu.

Koulutus rahan ansaitsemiseen Internetissä: bloggaaja, videobloggaaja, ohjelmat, verkkosivustot, verkkokauppa, artikkelit, kirjat jne.

Voit tukea sivuston kehittämistä, maksaa Andrey Georgievich Olshevskyn konsultointipalveluista

10.15.17 Olševski Andrei Georgievichsähköposti:[sähköposti suojattu]

Vektorialgebra

Määritelmä:

Vektori on suunnattu segmentti tasossa tai avaruudessa.

Ominaisuudet:

1) vektorin pituus

Määritelmä:

Kahta vektoria kutsutaan kollineaariseksi, jos ne sijaitsevat yhdensuuntaisilla viivoilla.

Määritelmä:

Kahta kollineaarista vektoria kutsutaan samansuuntaisiksi, jos niiden suunnat ovat samat ( ) Muuten niitä kutsutaan vastakkaisiin suuntiin (↓ ).

Määritelmä:

Kaksi vektoria ovat yhtä suuret, jos ne ovat samansuuntaisia ja niillä on sama pituus.

Esimerkiksi,

Toiminnot:

1. Vektorin kertominen luvulla

Jos
, Tuo

↓Jos < 0

Nollavektorin suunta on mielivaltainen

Luvulla kertomisen ominaisuudet

2. Vektorin lisäys

Rinnakkaissääntö:

Lisäysominaisuudet:

- tällaisia vektoreita kutsutaan vastakkaisiksi toisiaan vastaan. Se on helppo nähdä

Yhteiset ominaisuudet:

NOIN määritelmä:

Kahden vektorin välinen kulma on kulma, joka saadaan, jos nämä vektorit piirretään yhdestä pisteestä, 0    

3. Vektorien pistetulo.

, Missä - vektorien välinen kulma

Vektorien skalaaritulon ominaisuudet:

1) (yhtälöt tapahtuvat vektorien vastakkaisen suunnan ja samansuuntaisten vektorien tapauksessa)

Jos
, silloin tuotteen merkki on positiivinen, Jos ↓Se on negatiivista

)

6), eli
, tai mikä tahansa vektoreista on nolla

Vektorien soveltaminen

MN – keskiviiva

Todista se

Todiste:

, vähennä vektori molemmilta puolilta
:

Todista, että rombin lävistäjät ovat kohtisuorassa

Todiste:

Löytö:

Ratkaisu:

Vektorien hajoaminen emäksiksi.

Määritelmä:

Lineaarinen vektoreiden yhdistelmä (LCV) on muodon summa

(LKV)

Missä 1 ,  2 , …  s – mielivaltainen numerosarja

Määritelmä:

LCI:n sanotaan olevan ei-triviaali i = 0, muuten sitä kutsutaan ei-triviaaliksi.

Seuraus:

Ei-triviaalilla LCV:lla on vähintään yksi nollasta poikkeava kerroin Vastaanottaja  0

Määritelmä:

Vektorijärjestelmä
kutsutaan lineaarisesti riippumattomaksi (LNI),Jos() = 0  Kaikki i  0,

eli vain sen triviaali LC on yhtä suuri kuin nolla.

Seuraus:

Lineaarisesti riippumattomien vektoreiden ei-triviaali LC on nollasta poikkeava

Esimerkkejä:

1)
- LNZ

2) Anna Ja makaa sitten samassa tasossa
- LNZ , ei-kollineaarinen

3) Anna , , eivät kuulu samaan tasoon, niin ne muodostavat LNZ-vektorijärjestelmän

Lause:

Jos vektorijärjestelmä on lineaarisesti riippumaton, niin ainakin yksi niistä on muiden lineaarinen yhdistelmä.

Todiste:

 Antaa () = 0 eikä kaikki minä ovat yhtä kuin nolla. Yleisyyttä menettämättä, anna s  0. Sitten
, ja tämä on lineaarinen yhdistelmä.

 Antaa

Siis LZ.

Lause:

Kaikki 3 vektoria tasossa ovat lineaarisesti riippuvaisia.

Todiste:

Olkoon vektorit annettu
, mahdolliset tapaukset:

1)


2) ei-kollineaarinen

Ilmaistaan se kautta ja:
, missä
- ei-triviaali LC.

Lause:

Antaa
- LZ

Silloin mikä tahansa "laajempi" järjestelmä on LZ

Todiste:

Koska - LZ, niin siellä on ainakin yksi i  0 ja () = 0

Sitten ja () = 0

Määritelmä:

Lineaarisesti riippumattomien vektoreiden järjestelmää kutsutaan maksimaaliseksi, jos siihen lisätään jokin muu vektori, josta tulee lineaarisesti riippuvainen.

Määritelmä:

Avaruuden ulottuvuus (taso) on vektorien lukumäärä maksimaalisessa lineaarisesti riippumattomassa vektorijärjestelmässä.

Määritelmä:

Kanta on mikä tahansa järjestetty maksimaalinen lineaarisesti riippumaton vektorijärjestelmä.

Määritelmä:

Kanta kutsutaan normalisoiduksi, jos siihen sisältyvien vektorien pituus on yksi.

Määritelmä:

Kanta kutsutaan ortogonaaliksi, jos kaikki sen elementit (vektorit) ovat pareittain kohtisuorassa.

Lause:

Ortogonaalisten vektorien järjestelmä on aina lineaarisesti riippumaton (jos nollavektoreita ei ole).

Todiste:

Antaa olla järjestelmä ortogonaaliset vektorit (ei nolla), eli
. Oletetaan , Kerromme tämän LC:n skalaarisesti vektorilla :

Ensimmäinen hakasulku on nollasta poikkeava (vektorin pituuden neliö), ja kaikki muut hakasulkeet ovat ehdon mukaan nollaa. Sitten 1 = 0. Vastaavasti 2 …  s

Lause:

Olkoon M = - kanta. Sitten voimme esittää minkä tahansa vektorin muodossa:

missä ovat kertoimet 2 …  s määritetään yksiselitteisesti (nämä ovat vektorin koordinaatit kantaan M nähden).

Todiste:

1)
=
- LZ (perusehdon mukaan)

sitten - ei-triviaali

A) 0 = 0, mikä on mahdotonta, koska käy ilmi, että M – LZ

b) 0  0

jaettuna 0

nuo. siellä on henkilökohtainen tili

2) Todistetaan se ristiriitaisesti. Olkoon vektorin toinen esitys (ts. ainakin yksi pari
). Vähennetään kaavat toisistaan:

- LC on ei-triviaali.

Mutta ehdon mukaan - perusteella ristiriita, eli hajoaminen on ainutlaatuinen.

Johtopäätös:

Jokainen kanta M määrittää yksi-yhteen vastaavuuden vektorien ja niiden koordinaattien välillä suhteessa kantaan M.

Nimitykset:

M = - mielivaltainen vektori

Sitten

Lineaarisen yhdistelmän kertoimien ainutlaatuisuus todistetaan samalla tavalla kuin edellisessä seurauksessa.

Seuraus: Mitkä tahansa neljä vektoria ovat lineaarisesti riippuvaisia

Luku 4. Perusteen käsite. Vektorin ominaisuudet tietyssä kannassa

Määritelmä:Pohja avaruudessa on mikä tahansa järjestys ei-samantasoisten vektoreiden kolmois.

Määritelmä:Perusta koneeseen on mikä tahansa järjestys ei-kollineaaristen vektoreiden pari.

Kanta avaruudessa mahdollistaa jokaisen vektorin yksilöllisen assosioinnin järjestetyssä numeroiden kolmiossa - kertoimissa, jotka edustavat tätä vektoria kantavektoreiden lineaarisen yhdistelmän muodossa. Päinvastoin, yhdistämme vektorin jokaiseen järjestettävään lukukolmikkoon käyttämällä kantaa, jos teemme lineaarisen yhdistelmän.

Numeroita kutsutaan komponentit (tai koordinaatit ) vektori tietyssä kannassa (kirjoitettu ).

Lause: Kun lisäät kaksi vektoria, niiden koordinaatit lisätään. Kun vektori kerrotaan luvulla, kaikki vektorin koordinaatit kerrotaan tällä luvulla.

Todellakin, jos , Tuo

Vektorikoordinaattien määritelmä ja ominaisuudet tasossa ovat samanlaiset. Voit muotoilla ne helposti itse.

Luku 5. Vektoriprojektio

Alla vektorien välinen kulma tarkoittaa dataa vastaavien vektoreiden välistä kulmaa, jolla on yhteinen origo. Jos kulman referenssisuuntaa ei ole määritelty, niin vektorien väliseksi kulmaksi katsotaan se kulma, joka ei ylitä arvoa π. Jos yksi vektoreista on nolla, kulman katsotaan olevan nolla. Jos vektorien välinen kulma on suora, vektoreita kutsutaan ortogonaalinen .

Määritelmä:Ortogonaalinen projektio vektori vektorin suuntaan jota kutsutaan skalaarisuureeksi , φ – vektorien välinen kulma (kuva 9).

Tämän skalaarisuureen moduuli on yhtä suuri kuin segmentin pituus O.A. 0 .

Jos kulma φ on terävä, projektio on positiivinen; jos kulma φ on tylpä, projektio on negatiivinen; jos kulma φ on suora, projektio on nolla.

Ortogonaalisella projektiolla segmenttien välinen kulma O.A. 0 Ja A.A. 0 suoraan. On projektioita, joissa tämä kulma poikkeaa oikeasta kulmasta.

Vektorien projektioilla on seuraavat ominaisuudet:

Pohja on ns ortogonaalinen , jos sen vektorit ovat pareittain ortogonaalisia.

Ortogonaalista kantaa kutsutaan ortonormaali , jos sen vektorit ovat yhtä pitkiä kuin yksi. Avaruuden ortonormaalista perustasta käytetään usein merkintää.

Lause: Ortonormaalilla pohjalla vektorien koordinaatit ovat tämän vektorin vastaavat ortogonaaliset projektiot koordinaattivektoreiden suuntiin.

Esimerkki: Muodostakoon yksikköpituinen vektori kulman φ tasossa ortonormaalikantaisen vektorin kanssa, niin .

Esimerkki: Muodostakoon yksikköpituinen vektori kulmat α, β, γ vektorien , ja ortonormaalikannan kanssa avaruudessa, vastaavasti (kuva 11), sitten . Lisäksi. Suureita cosα, cosβ, cosγ kutsutaan vektorin suuntakosineiksi

Luku 6. Pistetuote

Määritelmä: Kahden vektorin skalaaritulo on luku, joka on yhtä suuri kuin näiden vektorien pituuksien ja niiden välisen kulman kosinin tulo. Jos yksi vektoreista on nolla, skalaaritulon katsotaan olevan nolla.

Vektorien skalaaritulo ja on merkitty [tai ; tai ]. Jos φ on vektorien välinen kulma ja , niin .

Skalaarituotteella on seuraavat ominaisuudet:

Lause: Ortogonaalisesti minkä tahansa vektorin komponentit löydetään kaavojen mukaan:

Todellakin, anna , ja jokainen termi on kollineaarinen vastaavaan perusvektoriin. Toisen osan lauseesta seuraa, että , jossa plus- tai miinusmerkki valitaan sen mukaan, ovatko vektorit , ja suunnattu samaan vai vastakkaiseen suuntaan. Mutta, , Jossa φ on vektorien välinen kulma ja . Niin, . Loput komponentit lasketaan samalla tavalla.

Skalaarituloa käytetään seuraavien perusongelmien ratkaisemiseen:

1. ; 2. ; 3. .

Annetaan vektorit tietyssä kannassa, ja sitten skalaaritulon ominaisuuksia käyttämällä voimme kirjoittaa:

Suureita kutsutaan tietyn kannan metrisiksi kertoimiksi. Siten .

Lause: Ortonormaalisesti

;
;
;
.

Kommentti: Kaikki argumentit tässä osiossa on annettu vektorien sijainnille avaruudessa. Tapaus, jossa vektorit sijaitsevat tasossa, saadaan poistamalla tarpeettomat komponentit. Kirjoittaja ehdottaa, että teet tämän itse.

Luku 7. Vektorituote

Ei-koplanaaristen vektorien järjestyttyä kolmiosaa kutsutaan oikealle suuntautunut (oikein ), jos lyhin käännös ensimmäisestä vektorista toiseen on näkyvissä vastapäivään yhteiseen alkupisteeseen soveltamisen jälkeen kolmannen vektorin päästä. Muussa tapauksessa kutsutaan järjestettyä ei-tasoisten vektorien kolmoisosaa vasemmalle suuntautunut (vasemmalle ).

Määritelmä: Vektorin ja vektorin ristitulo on vektori, joka täyttää ehdot: